基于全局可加模型的微合金钢力学性能预报方法与流程
本发明涉及冶金工业轧制过程数学模型,特别涉及基于全局可加模型的微合金钢力学性能预报方法。
背景技术:
为了满足社会需求和适应市场竞争,现代钢铁企业必须不断改善钢铁产品的组织性能,同时降低生产成本,缩短产品研发周期。这就需要改变以往昂贵而耗时的物理试验方法,借助先进的计算机辅助支撑工具来完成钢铁产品的设计。热轧带钢力学性能预报模型可用于热轧新产品设计和钢种优化,因此一直都是世界各国冶金工作者研究方向之一,与之相关的大量研究工作也一直在开展。
热轧带钢力学性能预报模型建立的理论依据是产品的力学性能决定于其内部组织,而组织又取决于带钢成分及其生产工艺,这两者与力学性能间存在确定而复杂的关系。力学性能预报模型就是要揭示这些参数之间的定量关系,从而根据这些参数来预报产品的力学性能。性能预报问题经过多年的研究,已取得了大量研究成果,国内外众多钢铁企业都试用或使用过性能预报系统,但现有模型在可靠性、实用性与外延性方面还存在不足,难以满足现场用户使用的要求。
从建模思路来看,性能预报问题建模思路大致分为两种:一种是机理建模,基于实验室物理冶金学的实验结果,建立数学模型来预测产品的力学性能;另一种是数据建模,根据实际生产数据,利用神经网络等智能算法来预测力学性能。以上两种建模方式均存在不足,机理建模多以钢种为单位进行研究,存在不能覆盖众多钢种的局限性,也不便研究成分、工艺对组织性能的影响规律,计算精度不够;而数据建模的缺陷在于:建立的模型存在不确定性,无法保证外推能力(外延性),对训练样本精度高,但难以适应未经过训练的数据样本。
技术实现要素:
本发明是为了解决上述问题而进行的,目的在于提供一种可靠性高、外延性强、实用性广的基于全局可加模型的微合金钢力学性能预报方法。
本发明提供的基于全局可加模型的微合金钢力学性能预报方法,具有这样的特征,包括以下步骤:
步骤a,确定微合金钢力学性能预报模型的影响因素;
步骤b,计算微合金钢轧制过程中析出的碳氮化物成分及含量;
步骤c,根据广义可加模型理论,将微合金钢力学性能预报模型表达为若干个子模型的可加形式;
步骤d,估计微合金钢力学性能预报模型;以及
步骤e,验证子模型的可靠性。
本发明提供的基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,步骤a,具有以下步骤:
步骤a-1,根据冶金机理、数据采集的过程和先验知识将影响因素分为四大类:化学成分、工艺参数、检测参数、异常标记;以及
步骤a-2,分别在每个大类中寻找影响因素,
其中,步骤a-2,包含以下步骤:
步骤a-2-1,将一些公认的影响因素筛选出来;
步骤a-2-2,寻找可能会起显著作用的影响因素。
本发明提供的基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,步骤b,具有以下步骤:
步骤b-1,基于多元第二相固溶析出理论,开发能定量计算热轧过程中碳氮化物析出成分及含量的热力学模型,并考虑碳氮化物和aln的相互作用;
步骤b-2,对热力学模型进行求解,采用牛顿拉夫森算法进行数值求解,通过迭代求解过程,确定不同成分下的碳氮化物和aln的析出开始温度与析出顺序,最终获得微合金钢轧制过程中析出的碳氮化物成分及含量。
基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,步骤c,具有以下步骤:
微合金钢力学性能预报模型的基本形式为
其中,ts代表钢材的力学性能参数;α为截距;sj(·)为各自变量xj的三次光滑样条函数,同时也代表力学性能预报模型的各个子模型;p为自变量个数。
基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,步骤d,钢材力学性能预报模型的基本形式确定后,根据从现场收集的热轧过程数据,对微合金钢力学性能预报模型进行估计,
对三次光滑样条函数的估计,采用back-fitting算法,其具体实现过程如下:
初始化,令m=0:
迭代过程,令m=m+1:
终止:直到小于预定正值常数或循环次数达到指定次数。
本发明提供的基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,步骤e,当力学性能预报模型建好后,需要根据机理知识与生产数据来验证各子模型的可靠性。
本发明提供的基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,热力学模型为:
[ala][na]=kaln
kmc、kmn分别为纯碳化物和氮化物的固溶度积;[ma]、[ca]和[na]为固溶的各元素的摩尔分数;lcn=-4260j/mol,交互作用系数;r=8.314j/(k·mol),气体常数;t为绝对温度;m0、c0、n0为钢中微合金元素、碳元素及氮元素的摩尔分数;al0为钢中al的摩尔分数;fp为析出的碳氮化铌的摩尔分数;[ala]为奥氏体中固溶的al的摩尔分数;kain为aln的固溶度积;faln为析出的aln的摩尔分数。此外,kmc、kmn和kaln均为二元第二相的平衡固溶度积,表示为:
kmx=[ma][xa]=c×10a-b/t
式中:afe、am和ax分别为铁、微合金元素和间隙元素(碳元素或氮元素)的相对原子质量;a、b为固溶度积公式的系数。
本发明提供的基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,子模型包括两类:成分类子模型和工艺类子模型。
本发明提供的基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,间隙元素为碳元素。
本发明提供的基于全局可加模型的微合金钢力学性能预报方法,还具有这样的特征:其中,间隙元素为氮元素。
发明作用和效果
根据本发明所涉及基于全局可加模型的微合金钢力学性能预报方法,“全局”是指通过收集多个钢种的生产数据来建模,而不仅仅针对某个具体钢种;“可加”是指模型在形式上是可加的,采用广义可加模型的思路,将力学性能预报模型分解为多个子模型。
另外,需要考虑微合金元素碳氮化物析出对力学性能的影响,基于多元第二相固溶析出理论开发热力学模型,对不同温度、成分下的微合金钢轧制过程中碳氮化物析出成分及含量进行定量计算,将计算获得的碳氮化物析出成分、含量与微合金钢实际生产数据结合起来,建立可靠性高、外延性强、实用性广的力学性能预报模型。
上述技术方案获得的微合金钢产品力学性能预报模型具有计算精度高、适应范围广等优点,可用于微合金钢新产品设计和钢种优化,达到减少传统的物理试验次数,缩短产品研发周期,降低研发成本的目的。
附图说明
图1是本发明在实施例中的基于全局可加模型的微合金钢力学性能预报方法的流程图;
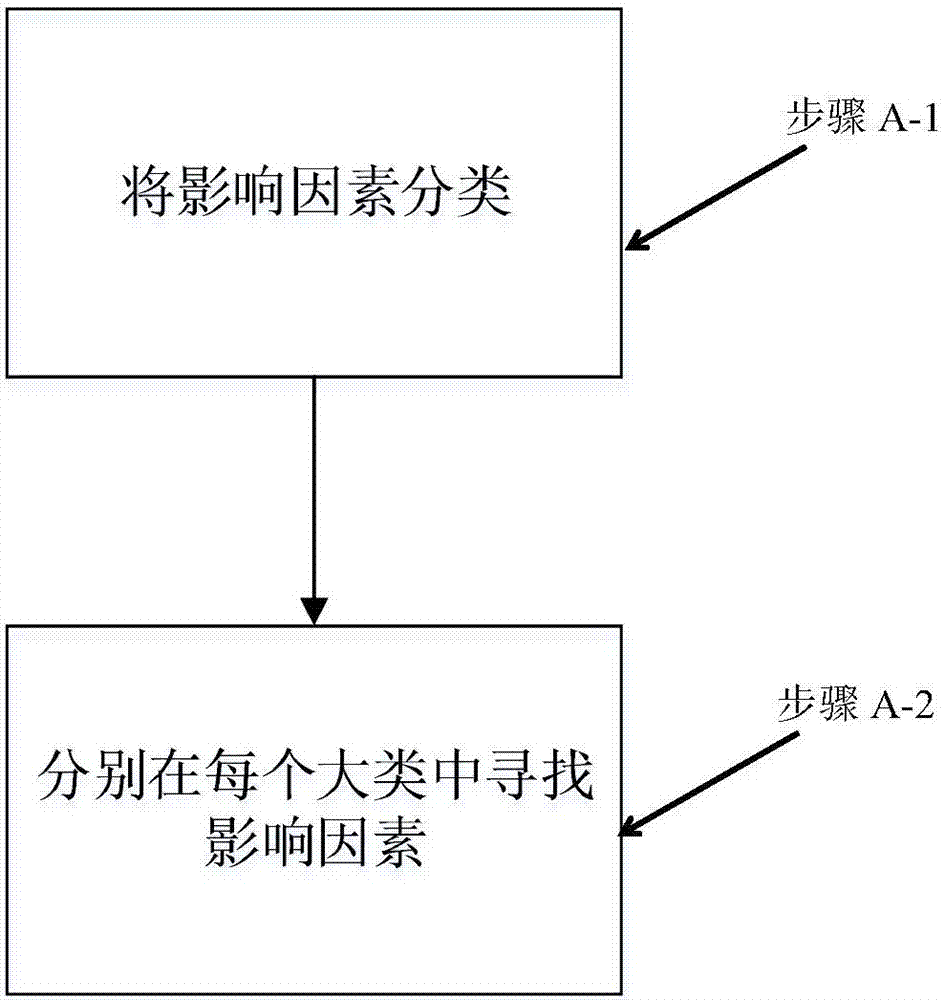
图2是本发明在实施例中的步骤a的流程图;
图3是本发明在实施例中的步骤a-2的流程图;
图4是本发明在实施例中的确定变量重要性的流程图;
图5是本发明在实施例中的微合金钢碳氮化合物析出的热力学数值计算流程;
图6(a)是本发明在实施例中的无aln析出的计算结果图;
图6(b)是本发明在实施例中的有aln析出的计算结果图;
图7(a)是本发明在实施例中的影响出抗拉强度ts的出炉温度的光滑函数图;
图7(b)是本发明在实施例中的影响出抗拉强度ts的卷取温度的光滑函数图;
图7(c)是本发明在实施例中的影响出抗拉强度ts的终轧厚度的光滑函数图;
图7(d)是本发明在实施例中的影响出抗拉强度ts的剩余碳(质量分数)的光滑函数图;
图7(e)是本发明在实施例中的影响出抗拉强度ts的硅(质量分数)的光滑函数图;
图7(f)是本发明在实施例中的影响出抗拉强度ts的锰(质量分数)的光滑函数图;
图7(g)是本发明在实施例中的影响出抗拉强度ts的碳化铌(质量分数)的光滑函数图;
图7(h)是本发明在实施例中的影响出抗拉强度ts的氮化铌(质量分数)的光滑函数图;
图8(a)是本发明在实施例中的力学性能预报模型的抗拉强度预测值与实测值的对比图;
图8(b)是本发明在实施例中的力学性能预报模型的屈服强度预测值与实测值的对比图。
具体实施方式
以下参照附图及实施例对本发明所涉及的基于全局可加模型的微合金钢力学性能预报方法作详细的描述。
实施例
下面以热连轧含nb微合金钢为例进行力学性能预报建模。
如图1、图2和图3所示,步骤a:确定微合金钢力学性能预报模型的影响因素,进入步骤b。
对力学性能预报过程参数进行工业大数据分析,寻找合适的影响因素。由于影响因素具有多样性、复杂性,因此影响因素的寻找过程是一个反复校正的过程。通过随机森林、贝叶斯方法等分析方法,同时结合冶金学机理及先验知识,选取带钢中碳、硅、锰、磷、铌等化学成分,以及出炉温度tf、粗轧温度tr、精轧入口温度tfe、终轧温度tfd、卷取温度tc、终轧厚度hfd等轧制工艺参数作为模型的影响因素(即自变量);抗拉强度、屈服强度等力学性能参数作为模型的响应变量。
影响力学性能的因素很多,而且部分变量之间存在交互作用。这就使得寻找影响因素时需要将冶金机理、统计方法与先验知识相结合。
步骤a-1:将影响因素分类:根据冶金机理、数据采集的过程和先验知识将影响因素分为四大类:化学成分、工艺参数、检测参数、异常标记。与检测相关的变量就是用于描述“数据是怎么来的”。如:取样机组、取样时间、取样方向、试样规格、屈服类型等等。当模型研究到一定的深度后,这些因素会成为限制模型精度和可靠度提升的主要因素。进入步骤a-2。
步骤a-2:分别在每个大类中寻找影响因素,具有以下步骤:
步骤a-2-1:将一些公认的影响因素筛选出来。例如:c、si、mn、n、nb、v、ti等成分,出炉温度、终轧温度、卷取温度、终轧厚度等工艺参数。然后,寻找可能会起显著作用的影响因素。图4为用随机森林判断一个变量重要性的流程图,根据变量的重要性来判断该变量是否起作用。值得注意的是:随机森林寻找的变量只是表示变量对数据具有较好的区分性,但是不能说明该变量对因变量一定有影响作用。由于数据的复杂性,寻找影响因素的过程是一个反复假设、分析、检验与修正的过程。
步骤b:计算微合金钢轧制过程中析出的碳氮化物成分及含量,进入步骤c。
步骤b-1:基于多元第二相固溶析出理论,开发能定量计算热轧过程中碳氮化物析出成分及含量的热力学模型,并考虑碳氮化物和aln的相互作用。对于fe-m-c-n合金体系的热力学模型如下:
上述式中:kmc、kmn分别为纯碳化物和氮化物的固溶度积;[ma]、[ca]和[na]为固溶的各元素的摩尔分数;lcn=-4260j/mol,交互作用系数;r=8.314j/(k·mol),气体常数;t为绝对温度;m0、c0、n0为钢中微合金元素、碳元素及氮元素的摩尔分数;fp为析出的碳氮化铌的摩尔分数。
对于存在aln析出的情况,由于其具有六方晶格结构,不溶于具有nacl结构的碳氮化合物而独立存在。对于fe-al-nb-c-n热力学平衡系统,需要将式(3)~(5)替换为下列式子:
[ala][na]=kaln(6)
上述式中:[ala]为奥氏体中固溶的al的摩尔分数;kain为aln的固溶度积;faln为析出的aln的摩尔分数;al0为钢中al的摩尔分数。此外,kmc、kmn和kaln均为二元第二相的平衡固溶度积,一般可统一表示为:
kmx=[ma][xa]=c×10a-b/t(11)
式中:afe、am和ax分别为铁、合金元素和间隙元素(碳元素或氮元素)的相对原子质量;a、b为固溶度积公式的系数。
步骤b-2:对上述热力学模型进行求解。由于上述热力学模型是一组非常复杂的非线性方程组,采用牛顿拉夫森算法进行数值求解,通过迭代求解过程,确定不同成分下的碳氮化物和aln的析出开始温度与析出顺序,最终获得微合金钢轧制过程中析出的碳氮化物成分及含量,计算流程如图5所示。
研究表明带钢中nb和c、n会在奥氏体相中析出形成碳氮化铌复合化合物,所以需要采用热力学模型计算出各卷带钢在轧制过程中析出的nbc、nbn含量,用质量分数来表示。
为了示例,图6(a)和图6(b)为其中2卷带钢的计算结果,图6(a)为无aln析出情况,图6(b)为有aln析出情况。
模型可自动根据带钢成分、温度计算是否存在aln的析出。为便于对比,各元素固溶质量分数采用相对于原始成分的比值来表示。
由图6(b)可见,随着温度的降低,固溶的n、nb元素的质量分数在不断减少,而析出的nbc、nbn的质量分数在不断增加;整个过程中,碳元素减少的速度很慢。通过上述计算,可以得到各卷带钢在奥氏体中析出的nbc、nbn的质量分数,再用于后续的力学性能预报建模研究。
步骤c:根据广义可加模型理论,将微合金钢力学性能预报模型表达为若干个子模型的可加形式,进入步骤d。
首先,简要介绍广义可加模型相关理论。广义可加模型是广义线性模型的非参数化拓展,通过对自变量用非参数函数形式来拟合估计响应变量与自变量间的关系,模型中每一个加性项使用单个光滑函数估计,在每一加性项中可以解释响应变量如何随自变量的变化而变化。其优点是可以处理高维数据中因变量与自变量之间的非线性关系,适于对数据进行探索性分析或寻找响应变量与自变量间是否存在依存关系。广义可加模型因其结构简单、灵活性与稳定性好等优点在许多学科领域得到了广泛应用,其数学表达可写为:
式中:μ为响应变量y的条件期望,μ=e(y|x1,x2,...,xp);g(·)为连接函数;α为截距;fj(·)为自变量xj的任意单变量函数;p为自变量个数。
对于钢材力学性能预报模型而言,连接函数可选择单位连接函数;依据自变量与响应变量之间的散点图,选取各自变量的单变量光滑函数的估计方法。鉴于三次光滑样条具有计算简单、稳定性好、收敛性有保证等优点,选择三次光滑样条估计方法。
综上分析,钢材力学性能预报模型的基本形式可写为:
其中,ts代表钢材的抗拉强度、屈服强度、延伸率等力学性能参数;α为截距;sj(·)为各自变量xj的三次光滑样条函数,同时也代表力学性能预报模型的各个子模型;p为自变量个数。
子模型大体包括两类:c、mn、si、p、nb、ti、v、mo、cr及相互作用产生的碳氮化合物等成分子模型;出炉温度、粗轧温度、精轧温度、卷取温度、厚度、规格等工艺子模型。
采用三次光滑样条来估计各自变量的单变量光滑函数,设置模型形式为:
式中:si(xi)为各自变量的三次光滑样条函数,主要包括tf、tr、tfe、tfd、tc、hfd、cs(剩余碳),以及si、mn、p、nbc、nbn等影响因素。
步骤d:估计微合金钢力学性能预报模型,进入步骤e。
钢材力学性能预报模型的基本形式确定后,根据从现场收集的大量热轧过程数据,对微合金钢力学性能预报模型进行估计,也就是通过估计算法来获得各个子模型的参数形式或非参数形式。
对各单变量光滑函数sj(xj)的估计,采用back-fitting算法,其具体实现过程如下:
初始化,令m=0:
迭代过程,令m=m+1:
终止:直到小于预定正值常数或循环次数达到指定次数。
设置back-fitting算法的循环次数为10,循环迭代计算结束时,求得α=539.16。下面给出抗拉强度ts主要影响因素的光滑函数图,如图7(a)、7(b)、7(c)、7(d)、7(e)、7(f)、7(g)、7(h)所示,它们代表了各因素对抗拉强度ts的影响规律。
步骤e:验证子模型的可靠性。
当力学性能预报模型建好后,需要根据冶金机理与生产数据来验证各子模型的可靠性,即验证用它获得的规律是否真实。真实的规律往往都具有可重复性。因此,在验证子模型的可靠性时,要紧紧抓住规律的可重复性,在不同的维度下验证它是否可以被数据重现,从而避免一些虚假规律的产生。如果用一个子模型获得的规律在大多数情况下都能够被数据重现或者找不到明显的证据证明这个规律是虚假的,那么就认为这个子模型是可靠的。反之,需要分析子模型失效的原因,重新修正子模型。
如图7(a)、7(b)、7(c)、7(d)、7(e)、7(f)、7(g)、7(h)所示:(1)抗拉强度随出炉温度的升高而增大,这是因为加热温度越高,固溶进奥氏体中的铌质量分数越多,后续降温过程中能析出的碳氮化物也越多;(2)抗拉强度随卷取温度的升高而降低,这是因为tc越高,则卷取时的相变温度和析出温度就越高,相变温度增加会减小相变驱动力,使组织粗化,从而降低强度;同时,析出物在较高的温度下更容易发生长大,降低析出强化效果;(3)终轧厚度的增加会导致抗拉强度降低,这是因为带钢厚度越薄,则在层流冷却过程中冷得越快,因而过冷奥氏体的转变温度降低,驱动力增加,相变后的组织变细;(4)剩余碳质量分数越大,则抗拉强度越大,这是因为碳元素有很强的固溶强化效果,含碳量增加使固溶强化作用增加;另外,碳元素明显增强奥氏体的稳定性,使过冷奥氏体转变温度降低,从而细化组织;(5)与碳元素类似,硅和锰元素也有固溶强化作用,同时也能增加奥氏体稳定性;(6)氮化铌、碳化铌析出物的质量分数越大,则抗拉强度越大,这是因为碳氮析出物从变形奥氏体的晶界处析出,钉扎晶界,阻碍奥氏体再结晶,从而保持了奥氏体的形变效果,为随后的铁素体相变提供更多的形核点,细化铁素体晶粒,起到细晶强化的作用。此外,图5也表明,碳、硅、锰、碳氮化铌等成分对抗拉强度的影响程度大于出炉温度、终轧厚度等轧制工艺参数的影响。
根据式(14)及图7(a)、7(b)、7(c)、7(d)、7(e)、7(f)、7(g)、7(h)中求得的各单变量光滑函数,可得到热轧含nb微合金钢抗拉强度的预报模型,其中成分、工艺各因素对应的函数值可根据图8中的样条函数插值得到。同样地,应用上述方法可得到屈服强度的预报模型。
采用上述模型,计算7740卷某热连轧机组生产的含nb微合金钢钢(含多钢种)的抗拉强度ts与屈服强度ys,模型预测值与实测值的对比如图8所示,表1为模型预报的均方根误差和平均误差me,表2为其中几卷带钢抗拉强度的中间计算结果。
表1模型预报的均方根误差和平均误差me
表2其中几卷带钢抗拉强度的中间计算结果
可见,得到的子模型均是符合已有经验和机理知识的,且新模型具有较高的预报精度;此外,计算过程无需人工修正,模型预测值偏离实测值均在一定范围内,模型具有较强的适应能力。
实施例的作用与效果
根据本实施例所涉及基于全局可加模型的微合金钢力学性能预报方法,“全局”是指通过收集多个钢种的生产数据来建模,而不仅仅针对某个具体钢种;“可加”是指模型在形式上是可加的,采用广义可加模型的思路,将力学性能预报模型分解为多个子模型。
另外,需要考虑微合金元素碳氮化物析出对力学性能的影响,基于多元第二相固溶析出理论开发热力学模型,对不同温度、成分下的微合金钢轧制过程中碳氮化物析出成分及含量进行定量计算,将计算获得的碳氮化物析出成分、含量与微合金钢实际生产数据结合起来,建立可靠性高、外延性强、实用性广的力学性能预报模型。
上述技术方案获得的微合金钢产品力学性能预报模型具有计算精度高、适应范围广等优点,可用于微合金钢新产品设计和钢种优化,达到减少传统的物理试验次数,缩短产品研发周期,降低研发成本的目的。
 汇聚全球材料牌号的数据库-钢铁之家
汇聚全球材料牌号的数据库
汇聚全球材料牌号的数据库-钢铁之家
汇聚全球材料牌号的数据库